Alavancas
Imagine a seguinte situação: você precisa levantar um saco cheio de mantimentos.
A massa total do saco é 120 kg. Poucas pessoas conseguem, e geralmente somente aquelas que se preparam para isso. Entretanto, no decorrer da história, as pessoas muitas vezes tiveram que levantar pedras ou objetos, e não contavam com máquinas para auxiliá-las.
Há mais de 22 séculos, um homem chamado Arquimedes (287 – 212 a.C.) encontrou um método extremamente simples para resolver esse problema: ele descobriu as alavancas.
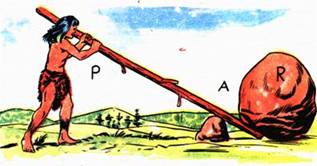
Uma alavanca nada mais é do que uma barra rígida que pode girar em torno de um ponto de apoio.
Em pleno século III a.C. Arquimedes afirmou: “Dê-me uma alavanca que moverei o mundo”
Como você poderia, com auxilio de uma alavanca, levantar um saco de 120 kg, fazendo uma força equivalente à que faria para levantar um saco de 20kg de arroz? Em outras palavras, como levantar uma massa com peso seis vezes maior que outra, fazendo a mesma força que faria para levantar essa?
Simples! É só a distância entre o ponto da barra rígida em que você aplica a força e o ponto de apoio (de P a A) ser seis vezes maior do que distância da massa até o ponto de apoio (de A a R).
Vamos denominar:
- Força resistente – é a força que queremos equilibrar. No exemplo acima, é o peso do saco de mantimentos.
- Força potente – é a força que sustentará a resistência. No exemplo, é a força que fazemos.
Tipos de alavancas
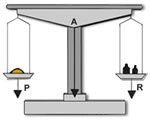
INTER-FIXA:
É quando o ponto apoio (A) está entre a aplicação da força potente (P) e a aplicação da força resistente (R).
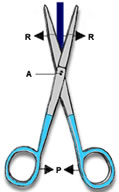
INTER-PONTENTE:
É quando a aplicação da força potente (P) está entre a aplicação da força resistente (R) e o ponto de apoio (A).
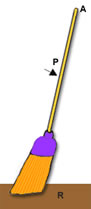
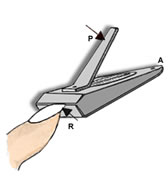
INTER-RESISTENTE:
É quando a aplicação da força resistente (R) está entre a aplicação da força potente (P) e o ponto de apoio (A).
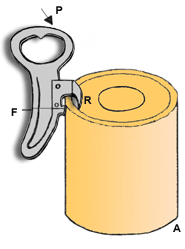
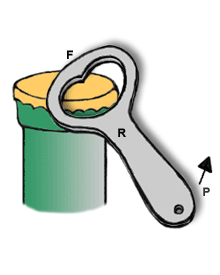
Equação das alavancas
Pediremos ajuda a matemática para encontrar uma expressão para a seguinte situação.
Equilibrar uma massa muito grande fazendo uma força bem menor que o peso dessa massa que queremos sustentar.
Vamos denominar:
R: valor da força resistente – a força que queremos equilibrar.
P: valor da força potente – é a força que sustentará a resistência.
BR: braço de resistência – é a distância do centro de gravidade do corpo ao ponto de apoio.
BP: braço de potência – é a distância do ponto de aplicação da força ao ponto de apoio.
O: Ponto de apoio
Verificamos que o equilíbrio será alcançado quando:
![]()
Exemplo de aplicação
Vamos calcular a força que um pedreiro tem de fazer para carregar 80 kg de terra com a ajuda de um carrinho de mão que possui 1,80 metros de comprimento. Sabendo que a distância entre o centro de gravidade do volume de terra até o centro da roda do carrinho é 90 cm.
Primeiramente vamos verificar qual tipo de alavanca temos.
Como o que fica no meio do carrinho é a terra, ou seja, a resistência, a alavanca é inter-resistente.
Temos:
braço de resistência = 90 cm = 0,9 m
braço de potência = 1,80 m
resistência = 80 kgf.
Portanto,
![]()
![]()
A interpretação física desse cálculo é a seguinte: o pedreiro necessita fazer uma força com intensidade de metade do peso do volume de terra para erguer o carrinho e transportar a carga.
Você percebeu a grande utilidade de uma máquina tão simples?





























